Cây chỉ số nhị phân - Cây Fenwick

Cây chỉ số nhị phân (Binary Indexed Tree) hay cây Fenwick (Fenwick Tree) là một CTDL giúp ta trả lời các truy vấn trên đoạn một cách hiệu quả. Mặc dù không “mạnh” bằng cây phân đoạn nhưng CTDL này vẫn được sử dụng thường xuyên trong lập trình thi đấu vì khả năng cài đặt nhanh và tính đơn giản của nó.

Ý tưởng

Ta có bài toán sau: cho một mảng \(a\) có \(n\) phần tử và \(q\) truy vấn có dạng (l, r). Với mỗi truy vấn, tìm và in ra tổng của các phần tử trong khoảng \([l, r]\). Chỉ số của mảng \(a\) bắt đầu từ \(1\).

\[a = [1, 5, 8, 2, 7, 3, 4, 6]\]

Nếu như giá trị của mảng không thay đổi thì ta có thể dễ dàng giải quyết bài toán bằng cách tạo một mảng \(T\) với \(T_0 = 0\), \(T_1 = a_1\) và \(T_i = T_{i - 1} + a_i\) với mọi \(i\) lớn hơn \(1\) (mảng \(T\) này còn được gọi là mảng cộng dồn).

\[T = [1, 6, 14, 16, 23, 26, 30, 36] \]

Khi này, ta có thể tính tổng các phần tử trong khoảng \([l, r]\) bằng công thức: \(query(l, r) = T_r - T_{l - 1}\).

Việc xây dựng mảng \(T\) có độ phức tạp \(O(n)\) và các truy vấn là \(O(1)\).

Tuy nhiên, nếu bài toán có các truy vấn yêu cầu ta cập nhật giá trị của một phần tử trong mảng (ví dụ như tăng giá trị của \(a_i\) lên \(x\) ) thì ta cần phải cập nhật giá trị ấy và xây dựng lại mảng \(T\) từ đầu đến cuối - một điều không hiệu quả nếu bài toán có nhiều truy vấn cập nhật giá trị.

Một ý tưởng tối ưu đó chính là ta chia mảng \(T\) thành hai đoạn con nhỏ hơn \(T1\) và \(T2\) - đoạn \(T1\) sẽ tính cộng dồn một nửa các phần tử đầu tiên trong mảng \(a\) còn đoạn \(T2\) sẽ tính cộng dồn các phần tử còn lại.

\[T1 = [1, 6, 14, 16], T2 = [7, 10, 14, 20] \]

Bằng cách này, khi cập nhật giá trị, ta chỉ cần tính lại một trong hai đoạn \(T1\) hoặc \(T2\).

Cốt lõi của cây Fenwick sẽ sử dụng ý tưởng này.

Cây Fenwick

Mặc dù có tên gọi là “cây” Fenwick nhưng CTDL này lại được biểu diễn trên một mảng dữ liệu.

Ta có mảng \(ft\). \(ft_i\) sẽ lưu tổng của các phần tử có chỉ số nằm trong khoảng \([i - LSB(i) + 1, i]\), với hàm \(LSB(i)\) trả về giá trị bit nhỏ nhất của \(i\). Ví dụ \(ft_6\) có giá trị bằng tổng của \(a_5\) và \(a_6\).

Từ đây, ta có mảng \(ft\) được xây dựng từ mảng \(a\):

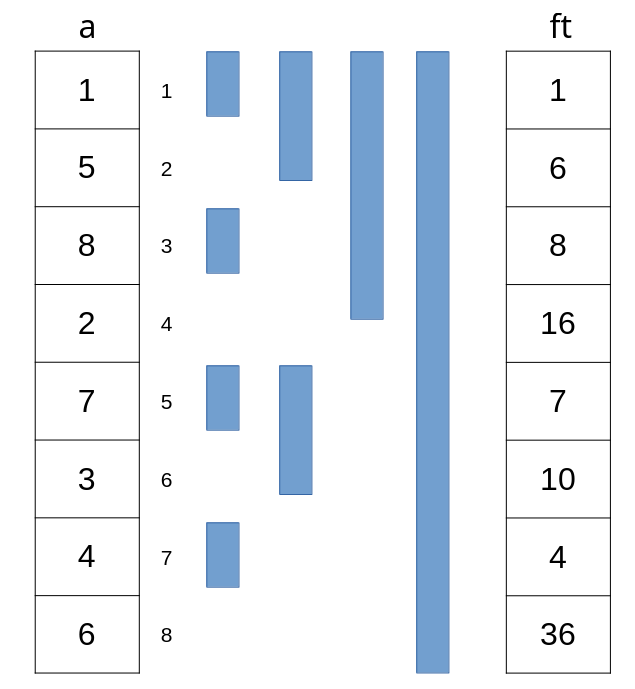
Ta sẽ sử dụng cây Fenwick vừa xây dựng để tìm kiếm đáp án.

Hàm sum(i)

Ta có hàm sum(i) tính tổng các phần tử từ \(1\) đến \(i\):

int sum(int i){
	int sum = 0;
	while(i > 0){
		sum += ft[i];
		i -= i & -i; // xóa LSB(i)
	}
	return sum;
}

Ta cũng có thể viết hàm sum(i) bằng cách sử dụng vòng lặp for:

int sum(int i){
	int sum = 0;
	for(; i > 0; i -= i & -i) sum += ft[i];
	return sum;
}

Hàm sum(i) này giúp ta có thể tính toán hiệu quả tổng của \(i\) số đầu tiên trong mảng \(a\). Từ đây ta có thể tính query(l, r) = sum(r) - sum(l - 1).

Vì với mỗi thao tác ta xóa \(LSB(i)\) khỏi \(i\) nên độ phức tạp của hàm sum bằng \(O(\log{n})\).

Thực tế trong hầu hết trường hợp số thao tác mà sum(i) thực hiện sẽ nhỏ hơn \(\log{i}\) do không phải lúc nào \(i\) cũng có \(\log{i}\) bit được bật.

Hàm update(i, x)

Ta có hàm update(i, x) tăng giá trị của phần tử \(a_i\) lên \(x\):

void update(int i, int x){
	while(i <= n){
		ft[i] += x;
		i += i & -i; 
	}
}

void update(int i, int x){
	for(; i <= n; i += i & -i) ft[i] += x;
}

Tương tự với sum(i), độ phức tạp của update(i, x) là \(O(\log{n})\).

Xây dựng mảng \(ft\)

Để xây dựng mảng \(ft\) cho cây Fenwick, ta có thể áp dụng \(1\) trong \(2\) phương pháp:

Phương pháp 1: gán \(ft_i = 0\) với mọi \(i\) từ \(1\) đến \(n\). Duyệt từ \(1\) đến \(n\), gọi hàm update(i, a[i]).

for(int i = 1; i <= n; ++i){
	update(i, a[i]);
}

Phương pháp \(1\) có độ phức tạp \(O(n\log{n})\).

Phương pháp 2: gán \(ft_i = a_i\) với mọi \(i\) từ \(1\) đến \(n\). Duyệt từ \(1\) đến \(n\), nếu \(i + LSB(i) \le n\), cập nhật \(ft_{i + LSB(i)} = ft_{i + LSB(i)} + ft_i\).

for(int i = 1; i <= n; ++i){
	ft[i] = a[i];
	int j = i + i & -i;
	if(j <= n) ft[j] += ft[i];
}

Phương pháp \(2\) có độ phức tạp \(O(n)\).

Cây Fenwick ngược

Một phương pháp cài đặt khác cho cây Fenwick chính là cây Fenwick ngược, với hàm ans(i) sẽ tính giá trị của đoạn \([i, n]\) thay vì \([1, i]\) như thông thường.

void update(int i, int x){
	for(; i > 0; i -= i & -i) ft[i] += x;
}
int sum(int i){
	int sum = 0;
	for(; i <= n; i += i & -i) sum += ft[i];
	return sum;
}

Độ phức tạp của các hàm trên cây Fenwick ngược cũng tương tự với các hàm ở Fenwick thường.